Randomly Decomposable Graphs, III (Some open questions)

Some open questions in RDGs

In this third post on randomly decomposable graphs, we explore some open questions accessible to undergraduate students.  Partial results on these questions, for selected graphs, have just begun to appear in the mathematical literature and there are many, many trails to be explored in this area of the mathematical wilderness!

Fix a graph H and explore the poset RD(H) of all graphs G which are randomly decomposable with respect to H.  Recall that the height of a graph G in this poset is the number of edge-disjoint copies of H required to make G.  If the height of G is the integer a  and if H has q edges then G has e=aq edges.  A graph G is abundant with respect to H if there are more than a copies of H in G; G is trivial with respect to H if there are exactly a copies of H in G.  Thus the poset RD(H) partitions into two sets, the set,  RD_0(H), of trivial randomly decomposable graphs, and the set RD_A(H) of abundant randomly decomposable graphs.  Since H itself is a trivial member of RD(H), we can ask for minimal members of RD_A(H), that is, graphs which are abundantly RDG but have no subgraphs which are.

With this brief review, some basic mathematical questions jump out at us.

1. Given a fixed graph H, classify completely the members of RD(H).
2. Given a fixed graph H, list the minimally abundant members of RD(H).
3. Classify graphs H for which there are no abundant RDGs, that is, for which RD(H)=RD_0(H).
4. Are there graphs H for which RD(H) is finite?  Indeed, is it possible that RD(H)={H} for some graphs?

The first two questions invite experimentation with small graphs.  Choose a graph H with just 3 or 4 edges and first attempt to find the smallest abundant members of RD(H).  A helpful result in this area is the following lemma: 

"If G is minimally abundant with respect to H then the height of G 

is bounded above by the number of edges of H."  

Thus if H has only three edges, one need use at most three copies of H in building these smallest abundant RDGs.

If it is relatively easy to describe the minimal elements in RD_A(H), maybe it is possible to describe all of RD(H).  This has been done for graphs with two edges, and for the graphs H=P_3 and H=K_3 with three edges.  It has also been done for a few small paths and should be done for graphs with three or four edges.  Although describing RD(H) is somewhat easy for a few graphs (like H=K_3) this gets surprisingly difficult for other graphs (like H=C_4.)

Some graphs cannot create abundant RDGs.  This is true for the complete graphs, H=K_n, in which there are too many edges to allow one to build up RDGs that have "extra" copies of H.  Are there other graphs with this property?  Surely there are ... so can we classify, in some way, those graphs for which every RDG is trivial?

If H is connected then the graph aH, consisting of a components, each isomorphic to H, is in RD(H) and so the poset RD_0(H) is infinite.  But if H is not connected, then maybe RD(H) could be finite? When is RD(H) finite?  

I can argue that if H is the graph with three edges on five vertices, below,  formed from the path of length two and a disconnected edge, then RD(H)={H}!  (That graph, H = P_2 + K_1, is drawn below, using output from the Sage software program.)

For the student just beginning to explore RDGs: take a notebook and pen (or pencil) and draw a small graph H with three or four edges.  You might wish to choose one of the graphs drawn below.

Then begin constructing members of RD(H).  See if you can develop the first few members of RD(H) that involve 2, 3 or 4 copies of H.  Can you detect a pattern?  Can you make a statement about trivial or abundant graphs?  Drop me a line at kenwsmith54 (at) gmail (dot) com!

[Mathematical prerequisites: This article requires a basic introduction to randomly decomposable graphs (as seen in the previous  few blog posts).]

Follow Ken W. Smith on Twitter @kenwsmith54

Randomly Decomposable Graphs, II, Paths

Abundant vs. trivial decompositions of a graph

In the previous post, we introduced randomly decomposable graphs, looking for the set, RD(H), of all graphs randomly decomposable with respect to a fixed graph H.

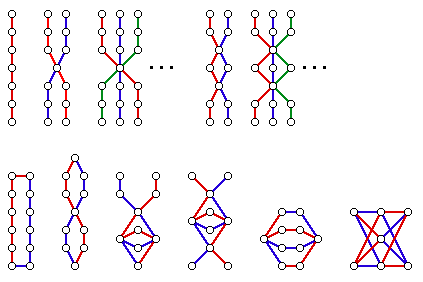
For example, if H is the path P_3, with four vertices and three edges, then there are five graphs, each with six edges which are in RD(H).  These five graphs include one disconnected graph, the graph which is two disconnected copies of P_3.  The four connected graphs are drawn below, with two edge-disjoint paths of length three drawn in different colors, one path in blue and another in red.  In each case, the removal of any path of length 3 leaves a path of length 3.

Note that although each of the graphs drawn above is clearly decomposable into two copies of P_3 (as indicated by the two colors, blue and red), there are LOTS more copies of P_3 in these graphs.  Indeed, the graph, C_6, on the left, has six copies of P_3, while the "bowtie" (second from the left) has (I think) eight copies of P_3, the complete graph K_4, third from left has six paths of length 3 and the rightmost graph (K_{2,3}) has 12.

Since there are so many copies of H in these graphs, it is not easy to show that these graphs are randomly decomposable.  On the other hand, if a graph G is constructed from  a  edge-disjoint copies of H and there are only  a  copies of H in G then the decomposition of G into copies of H is trivial.  For example, let us change H and set H to be the triangle (3-cycle) K_3, with 3 vertices and 3 edges.  Then the "bowtie" graph, above (second from the left), is trivially decomposable into copies of K_3 since it is the edge-disjoint union of  a=2 copies of K_3 and there are only two copies of K_3 in the graph.

If H has q edges and a graph G with e=qa edges decomposes into  a  edge-disjoint copies of H then we say G is trivially randomly decomposable with respect to H if there are only a copies of H in G.  If, instead, G has more than  a  copies of H, then we say that H is abundant in G.

The four graphs in the figure at the top of this blog all have H=P_3 as an "abundant" subgraph since  a=2 but there are, in each case, more than two copies of P_3.  On the other hand, if H=K_3, the bowtie graph is trivially decomposable since the two copies of K_3 used to construct the bowtie are the only copies of K_3 in the graph.

We make the distinction between trivial decompositions and abundant decompositions simply because we are not really interested in trivial decompositions.  We want an interesting problem.  The randomly decomposable graphs which are trivially decomposable are not interesting but the abundant graphs are.

The poset of randomly decomposable graphs and its trivial/abundant pieces

The set of finite graphs form a partially ordered set ("poset") ordered by the concept of subgraph. So the set RD(H) will also be a poset, with one member, G1, being less than another, G2, if G1 is a subgraph of G2.  It should be clear that this poset can be arranged by the height  a; at the bottom of the poset is H, immediately above H are the graphs which can be constructed from two copies of H; above those are the graphs constructed from three copies of H and so on.

If G1 is below G2 in the poset of randomly decomposable graphs (RDGs), then if G2 is trivially decomposable, so is G1.  The concept of "trivially" randomly decomposable is preserved by going down in the poset and so it is natural to ask if there are any maximally trivial RDGs.  These would be graphs which are trivially randomly decomposable but no graph above them is.

In a similar way, the concept of "abundantly" decomposable is preserved by going up the poset of RDGs, adding copies of H to graphs on a lower level.  If G1 is below G2 in the poset of RDGs, then if G1 is "abundant", so is G2.  Now H is trivial, not abundant, so given an abundant graph, we can always work ourselves down the poset of RDGs, removing a copy of H each time, until we reach a minimally abundant RDG, one which has no abundant subgraphs.  Thus minimally abundant RDGs sit at the cusp of "trivial" (uninteresting) RDGs and "abundant" (and complicated) RDGs.

Paths

We might begin our study of RDGs by beginning with the simplest graphs, the paths.  If P_n is a path of length n (and so has n+1 vertices and n edges) then what does RD(P_n) look like?  Since P_n is a connected graph, then if G is in RD(P_n), each connected component of G is also in RD(P_n) and so we can just concentrate on the connected members of RD(P_n).  There are only five connected members of RD(P_3).  They are:

The set RD(P_3) is then just a union of a finite number of copies of graphs from the set above. The four graphs on the left are of height 2; the rightmost graph is just H=P_3.  The poset RD(P_3) is infinite; a graph in that set is "abundant" if at least one of its components is from the first four graphs drawn on the left.  (Stated another way, a graph in RD(P_3) is "trivial" only if it is a disconnected union of copies of P_3.)

Below, off the webpage of Robert Molina (Alma College), in collaboration with Myles McNally (also at Alma) is a summary of all connected members of RD(P_4):

Since the number of edges in P_4 is even, there is an infinite set of connected graphs in which the paths are all joined in the middle.  This infinite set is represented by the three dots.

Here, from work of McNally & Molina, are the connected members of RD(P_5).  Note that this set is finite.  The first three graphs are predictable (to me) but the last two are rather strange. 

And here the connected members of RD(P_6).  Since the number of edges is even, we have some infinite families

but then a few more strange objects towards the end.

If H=P_7 then we have one infinite family (involving paths pinched at two points); we have the cycle and a figure eight ... and then ten more strange objects that would be hard to find without a computer.

H=P_8 is more of the same:

By the time our paths have 9 edges, the members of RD(P_9) are too many to draw here.  A few are given below.

All the members of RD(P_9) are available on the webpages maintained by McNally & Molina.  Picture of RD(P_9), RD(P_10) can be found at http://othello.alma.edu/~molina/rd(pk).html.  These graphs include collections of objects McNally & Molina call "braids", "twisted braids" and "branch growths."

And we have only begun looking at paths!!  What if H is more complicated?!

The Two-Path Conjecture

Along the way, as a number of us looked at RD(H) where H was a path, we began to believe that anytime we connected two copies of the path P_n, there were always additional copies of P_n created in that process.  No connected member of RD(P_n) of height two was trivial.  This eventually became a conjecture: 

The two-path conjecture.  Let G be the connected edge-disjoint union of two paths of length n. Then there are more than two copies of P_n in G.

With the help of Doug West and Herb Fleischner, we were able to prove that conjecture and publish the result.  (That paper is available here or here.)

and Erdos numbers

Many mathematicians encourage collaboration by keeping track of the "collaboration graph", in which two mathematicians are joined by an edge if they have collaborated on a published paper.  By tradition, the center of this collaboration graph is Paul Erdos.  It so happens that Doug West has Erdős number 1 so any other author of the paper on the Two-Path Conjecture has Erdos number 2. So I have Erdos number 2. (As it happens, I had earlier co-authored a paper with Allen Schwenk, who wrote a paper with Erdos, so I already had Erdos number 2.)

So ... if your Erdos number is higher than 3 (or does not yet exist!) you can get an Erdos number of 3 by publishing with me!  ;-)  Pick one of our open problems on one of these blogs, play with it a bit and write me an email.  Let's take a hike together in the mathematical wilderness!

Next time: RDGs, Part 3, some open questions in randomly decomposable graphs

[Mathematical prerequisites: This article requires a basic introduction to graph theory (as seen in the previous blog post).]

Follow Ken W. Smith on Twitter @kenwsmith54

Randomly decomposable graphs

The study of "randomly decomposable graphs" requires almost no mathematical background but can quickly lead to some interesting questions whose solutions require hard work and creativity.  I enjoy introducing this research area to students without a deep college math background.  Once the students become intrigued with this problem, they are ready to explore some other, deeper subjects!  (We will explore other, much deeper math topics in later blog posts.)

Edge decompositions of graphs

A graph, such as the cycle of 4 vertices, can be decomposed into two edge-disjoint copies of the path of length two.

This can be done is several different ways.

The bipartite graph K_{2,3} can be decomposed into three edge-disjoint copies of the path of length two.

But when we attempt to decompose this graph with six edges into three copies of the path of length two, we have to be careful how we do it.  If we start wrong, we may discover that we cannot finish the decomposition into three graphs all of which are paths.  For example, in the drawing below, we might remove the blue path of length two and then the black path of length two.  When we do that, we are left with the two reds edges which are not a path!

A general question in the decomposition of graphs begins with a fixed graph H and a larger graph G, where the edges of the graph G can be colored in such a way that each subgraph of a fixed color is isomorphic to H.  If H is the path of length two, all of the examples above give decompositions of a larger graph G into copies of H.

If the subgraph H has q edges then the number of edges in an H-decomposable graph G will be a multiple of q, say e=qa.  The integer a indicates the height of the graph G as a collection of copies of H.  The graph H, itself, has height 1; put together two copies of H to get a graph of height 2, and so on.  The cycle C_4 in the first drawing, above, has height 2 as a P_2-decomposable graph while K_{2,3} has height 3.

The theory of edge decompositions of graphs is a large field of mathematical research.  One may find it the subject of blog posts (here). There is at least one book (by ) published on the subject (which I found in my university library) and there is a study of infinite graphs and their simplicial decompositions (by Diestel).  A nice introduction to the subject is in this brief survey paper (pdf) by Fan Chung and Ron Graham.

Randomly decomposable graphs

If G is decomposable into edge-disjoints copies of a graph H then we say G is H-decomposable.  A partition of edges, each partition giving the subgraph H, is call an H-decomposition.

In 1985, the Chilean mathematician Sergio Ruiz dealt with questions about graphs decompositions which remain decompositions even when the target subgraph H is "randomly" (or "thoughtlessly") removed.  Given a fixed graph H, which graphs G are not just decomposable into copies of H but are decomposable in such a way that the decomposition cannot be "messed up".

For example, the cycle C_4 in the top picture is randomly decomposable into copies of H=P_2 while the bipartite graph K_{2,3} in the second and third pictures, is decomposable into copies of P_2, but is not "randomly" decomposable.  The third picture shows a decomposition which fails.

The formal definition of randomly decomposable is the following.  A graph G which is decomposable into copies of H is said to be randomly decomposable if the removal of the edges from any disjoint collection of copies of H leaves a graph which is still H-decomposable.  We say that G is an RD with respect to H.

For example, if H=P_2 is the path of length 2 then the graph G=K_{2,3} fails the "randomly" decomposable requirement since if we remove -- in the third picture -- the black path 3-2-4 and the blue path 3-1-5, we get a graph which does not even involve a copy of H.  So also C_4 is RD with respect to P_2, the graph K_{2,3} is not.

We can create a recursive definition equivalent to the one given above.  (The first definition, above, is due to Ruiz.)  The recursive definition defines the graph H to be "randomly" decomposable (of course) and then defines a graph G to be randomly decomposable if the removal of any copy of H leaves a randomly decomposable graph.  This recursive definition suggests that we construct randomly decomposable graphs beginning with graphs of low height and adding copies of H, checking the "randomly" condition as we go.

Let us construct graphs which are randomly decomposable with respect to H=P_2, the path with just two edges.  Pick a copy of H and label the vertices 1, 2 and 3 and assume the edges are {1,2} and {2,3} (so that H is the path 1-2-3.) Now take a second copy of H and assume the vertices are labelled a1, a2, a3 with a1 adjacent to a2 which is adjacent to a3. We may construct various P_2-decomposable graphs of height 2 by identifying certain vertices from the two copies.

First, if the vertices 1, 2, 3, a1, a2, a3 are all distinct, then the graph G is just two disconnected copies of H and so is clearly randomly decomposable.

If we identify the vertex 2 with the vertex a2 then we get the "star" with center 2 and end vertices 1,3, a1, a3.  This graph, often written K_{1,4}, is randomly decomposable.

If we identify the vertex 1 with a1 and the vertex 3 with a3, we instead get the 4-cycle drawn in the first figure. This graph is randomly decomposable.

One can consider other ways to put together two copies of H=P_2, but all of those choices lead to graphs which although decompose into copies of P_2, do not decompose randomly!  For example, if we just identify the vertices 1 and a1, we get a path 3-2-1-a2-a3 of length 4.  This graph is not randomly decomposable since we could remove the path 2-1-a2 and be left with a graph which is not isomorphic to H.

Randomly decomposable graphs where H is a path

When I first heard Sergio Ruiz speak on this topic, I thought it should be fairly easy to find all randomly decomposable graphs in which the subgraph H is a path.  But that turned out to be more complicated than I believed.  For example, suppose H is a path of length 7.  Then the graphs in the figure below are all RD with respect to H.  And this is just height 2!!

I offer a brief exercise to test these RD ideas, prior to my next post:

Find all graphs which are RD with respect to the path of length 3 and have height two.  (Feel free to stop at height two, using just two copies of P_3.)  

I will give the solution to that exercise next time.

Next time: Randomly decomposable graphs, 2 (paths and related subgraphs)