Randomly decomposable graphs, II (concentrating on paths)

Abundant vs. trivial decompositions of a graph

In the previous post, we introduced randomly decomposable graphs, looking for the set, RD(H), of all graphs randomly decomposable with respect to a fixed graph H.

For example, if H is the path P_3, with four vertices and three edges, then there are five graphs, each with six edges which are in RD(H).  These five graphs include one disconnected graph, the graph which is two disconnected copies of P_3.  The four connected graphs are drawn below, with two edge-disjoint paths of length three drawn in different colors, one path in blue and another in red.  In each case, the removal of any path of length 3 leaves a path of length 3.

Note that although each of the graphs drawn above is clearly decomposable into two copies of P_3 (as indicated by the two colors, blue and red), there are LOTS more copies of P_3 in these graphs.  Indeed, the graph, C_6, on the left, has six copies of P_3, while the "bowtie" (second from the left) has (I think) eight copies of P_3, the complete graph K_4, third from left has six paths of length 3 and the rightmost graph (K_{2,3}) has 12.

Since there are so many copies of H in these graphs, it is not easy to show that these graphs are randomly decomposable.  On the other hand, if a graph G is constructed from  a  edge-disjoint copies of H and there are only  a  copies of H in G then the decomposition of G into copies of H is trivial.  For example, let us change H and set H to be the triangle (3-cycle) K_3, with 3 vertices and 3 edges.  Then the "bowtie" graph, above (second from the left), is trivially decomposable into copies of K_3 since it is the edge-disjoint union of  a=2 copies of K_3 and there are only two copies of K_3 in the graph.

If H has q edges and a graph G with e=qa edges decomposes into  a  edge-disjoint copies of H then we say G is trivially randomly decomposable with respect to H if there are only a copies of H in G.  If, instead, G has more than  a  copies of H, then we say that H is abundant in G.

The four graphs in the figure at the top of this blog all have H=P_3 as an "abundant" subgraph since  a=2 but there are, in each case, more than two copies of P_3.  On the other hand, if H=K_3, the bowtie graph is trivially decomposable since the two copies of K_3 used to construct the bowtie are the only copies of K_3 in the graph.

We make the distinction between trivial decompositions and abundant decompositions simply because we are not really interested in trivial decompositions.  We want an interesting problem.  The randomly decomposable graphs which are trivially decomposable are not interesting but the abundant graphs are.

The poset of randomly decomposable graphs and its trivial/abundant pieces

The set of finite graphs form a partially ordered set ("poset") ordered by the concept of subgraph. So the set RD(H) will also be a poset, with one member, G1, being less than another, G2, if G1 is a subgraph of G2.  It should be clear that this poset can be arranged by the height  a; at the bottom of the poset is H, immediately above H are the graphs which can be constructed from two copies of H; above those are the graphs constructed from three copies of H and so on.

If G1 is below G2 in the poset of randomly decomposable graphs (RDGs), then if G2 is trivially decomposable, so is G1.  The concept of "trivially" randomly decomposable is preserved by going down in the poset and so it is natural to ask if there are any maximally trivial RDGs.  These would be graphs which are trivially randomly decomposable but no graph above them is.

In a similar way, the concept of "abundantly" decomposable is preserved by going up the poset of RDGs, adding copies of H to graphs on a lower level.  If G1 is below G2 in the poset of RDGs, then if G1 is "abundant", so is G2.  Now H is trivial, not abundant, so given an abundant graph, we can always work ourselves down the poset of RDGs, removing a copy of H each time, until we reach a minimally abundant RDG, one which has no abundant subgraphs.  Thus minimally abundant RDGs sit at the cusp of "trivial" (uninteresting) RDGs and "abundant" (and complicated) RDGs.

Paths

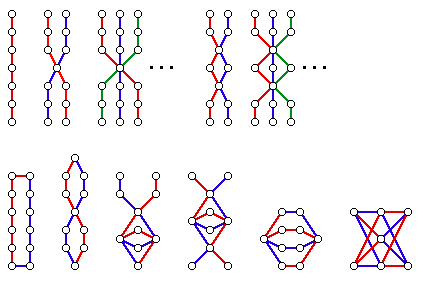
We might begin our study of RDGs by beginning with the simplest graphs, the paths.  If P_n is a path of length n (and so has n+1 vertices and n edges) then what does RD(P_n) look like?  Since P_n is a connected graph, then if G is in RD(P_n), each connected component of G is also in RD(P_n) and so we can just concentrate on the connected members of RD(P_n).  There are only five connected members of RD(P_3).  They are:

The set RD(P_3) is then just a union of a finite number of copies of graphs from the set above. The four graphs on the left are of height 2; the rightmost graph is just H=P_3.  The poset RD(P_3) is infinite; a graph in that set is "abundant" if at least one of its components is from the first four graphs drawn on the left.  (Stated another way, a graph in RD(P_3) is "trivial" only if it is a disconnected union of copies of P_3.)

Below, off the webpage of Robert Molina (Alma College), in collaboration with Myles McNally (also at Alma) is a summary of all connected members of RD(P_4):

Since the number of edges in P_4 is even, there is an infinite set of connected graphs in which the paths are all joined in the middle.  This infinite set is represented by the three dots.

Here, from work of McNally & Molina, are the connected members of RD(P_5).  Note that this set is finite.  The first three graphs are predictable (to me) but the last two are rather strange. 

And here the connected members of RD(P_6).  Since the number of edges is even, we have some infinite families

but then a few more strange objects towards the end.

If H=P_7 then we have one infinite family (involving paths pinched at two points); we have the cycle and a figure eight ... and then ten more strange objects that would be hard to find without a computer.

H=P_8 is more of the same:

By the time our paths have 9 edges, the members of RD(P_9) are too many to draw here.  A few are given below.

All the members of RD(P_9) are available on the webpages maintained by McNally & Molina.  Picture of RD(P_9), RD(P_10) can be found at http://othello.alma.edu/~molina/rd(pk).html.  These graphs include collections of objects McNally & Molina call "braids", "twisted braids" and "branch growths."

And we have only begun looking at paths!!  What if H is more complicated?!

The Two-Path Conjecture

Along the way, as a number of us looked at RD(H) where H was a path, we began to believe that anytime we connected two copies of the path P_n, there were always additional copies of P_n created in that process.  No connected member of RD(P_n) of height two was trivial.  This eventually became a conjecture: 

The two-path conjecture.  Let G be the connected edge-disjoint union of two paths of length n. Then there are more than two copies of P_n in G.

With the help of Doug West and Herb Fleischner, we were able to prove that conjecture and publish the result.  (That paper is available here or here.)

and Erdos numbers

Many mathematicians encourage collaboration by keeping track of the "collaboration graph", in which two mathematicians are joined by an edge if they have collaborated on a published paper.  By tradition, the center of this collaboration graph is Paul Erdos.  It so happens that Doug West has Erdős number 1 so any other author of the paper on the Two-Path Conjecture has Erdos number 2. So I have Erdos number 2. (As it happens, I had earlier co-authored a paper with Allen Schwenk, who wrote a paper with Erdos, so I already had Erdos number 2.)

So ... if your Erdos number is higher than 3 (or does not yet exist!) you can get an Erdos number of 3 by publishing with me!  ;-)  Pick one of our open problems on one of these blogs, play with it a bit and write me an email.  Let's take a hike together in the mathematical wilderness!

Next time: RDGs, Part 3, some open questions in randomly decomposable graphs

[Mathematical prerequisites: This article requires a basic introduction to graph theory (as seen in the previous blog post).]

Follow Ken W. Smith on Twitter @kenwsmith54